こんにちは、いちもくです。
統計学と言われても「なんだか難しそうだし、自分とは無縁のものなんだろうな」なんて感じる人は多いはず。
特に文系の学部出身の人は、なおさらそう感じるのではないでしょうか。
そもそも統計学とは、ある1つの群のデータに対して、その性質を調べたり、もっと大きな未知のデータや未来のデータを推測するための学問です。
AIやビッグデータ時代が到来する中、無視することはできない重要な学問となってきました。
どれだけたくさんの情報（データ）を得ることができても、データはそのままでは理解しにくく、役に立たないものもあります。
集めたデータを分かりやすい表現に置き換えることで、初めて理解できるものに変わり「生きたデータ」となるんです。
データを生かすために必要なのが「統計学」。
そんな統計学をマンガでわかりやすく学べるのが「マンガでわかる 超カンタン統計学」です。
本書では、統計学をビジネスの世界でも応用できるように、統計学の基礎である平均、中央値、標準偏差、偏差値の出し方をはじめ、分布の王様である正規分布、カイ二乗検定から分析に必要な手法までを、マンガでわかりやすく解説してくれています。
数学が苦手な人でも、統計学の基本を分かりやすく学べる本。
今回は、そんな「マンガでわかる 超カンタン統計学」の必読ポイントを詳しく解説していきます。
マンガでビジネス書を読むメリット
読書の習慣がない人にとって、難解なビジネス書を1冊読むのは結構大変なこと。
読むだけでも大変なのに、本の要点をつかんで実践するとなると、かなりハードルが高いものです
そんな読書が苦手な人にぜひおすすめしたいのが、ビジネスコミックを活用すること。
ビジネスコミックとは、難解なビジネス書をマンガでわかりやすく解説した本です。
短い時間でサクサク読めるから、原著を読まなくてもポイントをつかめるのが魅力。
原著を読む前にビジネスコミックでポイントを押さえておけば、原著を読んだときに内容をカンタンに理解することができるんです。
「マンガでわかる 超カンタン統計学」のストーリー
主人公は、念願のアパレルメーカーに就職したばかりの二階堂千尋。
引用：マンガでわかる超カンタン統計学意気込んで初出社しますが、先輩社員からは
「そんなに頑張らなくていいと思うよ」
引用：マンガでわかる超カンタン統計学と意外な声が掛かります。
その理由は、なんと店舗の閉店が迫っているから。
千尋が配属された店舗は、お客さんがほとんど来ず、来てもチラ見するだけでまったく買ってもらえない状況。
引用：マンガでわかる超カンタン統計学店員たちも自分勝手に動いているので、おすすめするのは売りやすい定番商品ばかり。
千尋なりにさまざまなアイデアを提案するも、店長は全然話を聞いてくれません。
そんなことを姉の麗香に相談したところ、
引用：マンガでわかる超カンタン統計学相手を納得させるには、数字が必要
とアドバイスを受けます。
どうすれば、数字を使って相手を納得させ、動かすことができるのか。
その答えは、統計学を使うことだと麗香は断言します。
引用：マンガでわかる超カンタン統計学麗香から紹介されたのは、隣に住む幼馴染の五十嵐一平。
引用：マンガでわかる超カンタン統計学統計学を駆使するコンサルタントとして、雑誌で特集されるほど有名な若き天才経営コンサルタントです。
果たして千尋は、統計学を使って店舗閉店の危機を乗り越えることができるのでしょうか。
「マンガでわかる 超カンタン統計学」の必読ポイント
各章では
- 分布 データを線で捉えよ
- 分散 データの塊を真ん中と広がりで捉える
- 相関 2つの変数の関係
- 標本 限られたサンプルから母集団の真の値を推定する
- カイ二乗検定 カテゴリの差を調べる
- 回帰分析 最も代表的な予測方法
と、全部で6つのテーマが解説されています。
今回はその中でも、「分布 データを線で捉えよ」の必読ポイントを紹介していきます。
確率分布の発見
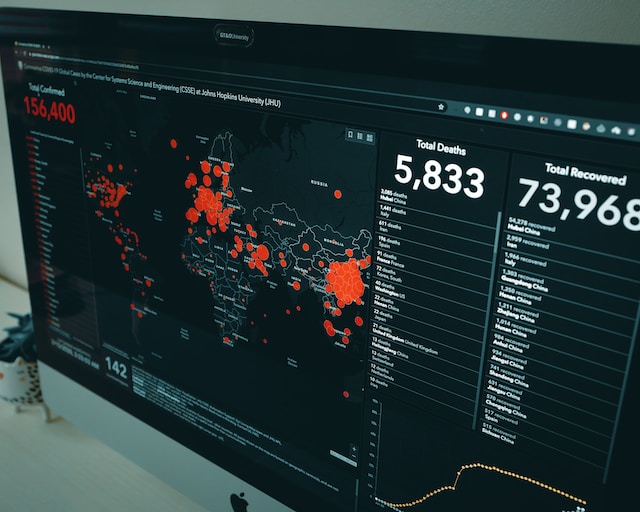
世の中には無数のデータがあります。
それらデータを集めたヒストグラムの形は、数少ないいくつかのパターンにまとまります。
データが集まってできたパターンのことを「分布」と呼びます。
より専門的には「確率分布」といいます。
データが集まるとパターンが生じるのが不思議ですが、その理由は
「データ（事象）の背後には、元になるメカニズム（法則）がある」
からだと考えられています。
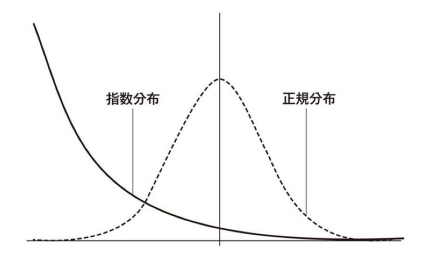
数ある分布をザックリ分けると
引用：マンガでわかる超カンタン統計学- 「釣り鐘型」 代表格は正規分布
- 「右下がり型」 代表格には指数分布とベキ分布
の2グループとなります。
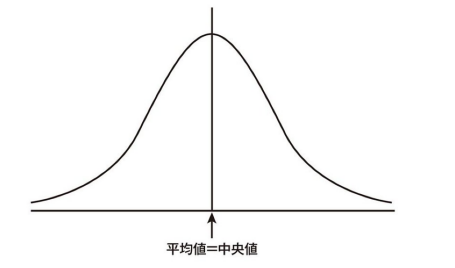
統計学では正規分布が主人公
引用：マンガでわかる超カンタン統計学正規分布は、世の中の至る所に顔をのぞかせる「分布の王様」です。
たとえば
大きな集団の身長、体重
学力テストの結果
などは、正規分布に従います。
なぜ、正規分布が広く見られるのでしょうか。
その理由は
でたらめなデータをたくさん足し合わせた結果は、ほとんどの場合、正規分布となる
からです。
たとえばサイコロを何度も転がして、出た目を足し合わせた結果が正規分布です。
サイコロは1から6の目が均等に出るので、足し合わせた結果がきれいにまとまる、というのは、感覚的にも分かると思います。
大雑把な表現ですが、
元データがどうであれ、たくさん足し合わせると、正規分布になる
というのが、正規分布の持つ強力な性質であり、正規分布が「正規」である理由です。
この性質は、数学の言葉で「中心極限定理」と名付けられています。
世の中には「正規分布」以外のデータもある
引用：マンガでわかる超カンタン統計学現在、統計学の教科書のほとんどは、正規分布が主人公です。
でも、世の中には正規分布以外のデータもあります。
身近なところでは、会社で扱うマーケティング・データや、貯蓄額といった社会党系には、正規分布ではないものが頻繁に現れます。
製品ごとの売り上げランキングや、ウェブサイトのアクセス数なども、多くの場合「右下がり型」です。
そうしたデータの外形を確認しないまま、すべて正規分布と捉えてしまうと、見当違いな結果になりかねません。
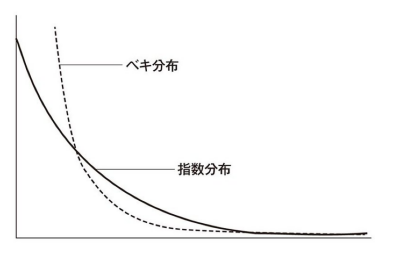
「右下がり型」でよく目にする分布として
- 指数分布
- ベキ分布
の2種類があります。
指数分布
指数分布とは、ざっくり言うとランダムなイベント（事象）の発生間隔を表す分布のこと。
貯金額の分布
昇進・昇段する人の人数
など。
日常的にはなじみが薄いかもしれませんが、
エネルギーをでたらめに配ったら指数分布になる
という事実から、物理・化学の世界では基本法則とみなされている分布です。
ベキ分布
「ベキ」は漢字で書くと「冪」となり、ある数の2乗・3乗といった冪乗のことを意味します。
音楽CDや書籍の売り上げランキング
ウェブサイトのアクセス頻度
などがベキ分布に従います。
指数分布と比べると、ベキ分布の方がいっそうグラフのカーブがきつく、けた外れに大きなデータを含んでいるのが特徴です。
ベキ分布が注目されるようになったきっかけは、インターネットが普及したから。
インターネット上でのアクセス数を比較すると、googleやYahoo!のようにきわめて大きな一部サイトと、少数のアクセスからなくたくさんのサイトに分かれます。
それらのアクセス数を集計すると、ベキ分布となることが判明したのです。
そのメカニズムは
口コミが口コミを呼ぶ
から。
あるサイトが新たに獲得するリンク数は、サイトの人気に比例すると考えます。
10個のサイトからリンクされている人気サイトは、1個のサイトからしかリンクされていないサイトに比べて、次のリンクを獲得するチャンスが10倍あるということになります。
この考え方で、たくさんのサイトに次々にリンクを張っていくと、出来上がったネットワーク全体のリンク数はベキ分布となります。
さいごに
本書ではこのほかにも
- 分散 データの塊を真ん中と広がりで捉える
- 相関 2つの変数の関係
- 標本 限られたサンプルから母集団の真の値を推定する
- カイ二乗検定 カテゴリの差を調べる
- 回帰分析 最も代表的な予測方法
など、統計学の基礎がマンガでわかりやすく解説されています。
統計学と言われても「なんだか難しそうだし、自分とは無縁のものなんだろうな」なんて感じる人は多いはず。
特に文系の学部出身の人は、なおさらそう感じるのではないでしょうか。
そもそも統計学とは、ある1つの群のデータに対して、その性質を調べたり、もっと大きな未知のデータや未来のデータを推測するための学問です。
AIやビッグデータ時代が到来する中、無視することはできない重要な学問となってきました。
どれだけたくさんの情報（データ）を得ることができても、データはそのままでは理解しにくく、役に立たないものもあります。
集めたデータを分かりやすい表現に置き換えることで、初めて理解できるものに変わり「生きたデータ」となるんです。
「マンガでわかる 超カンタン統計学」を読めば、数学が苦手な人でも、統計学の基本をマンガでわかりやすく学ぶことができますよ。
それじゃ、またね。
コメントを投稿するにはログインしてください。